大家知道,圆是平面几何中一个美丽的图形,而所有三角形都隐有一个外接圆。我们常常会通过找隐圆、制造圆、作辅圆等方法来求解相应的几何问题。今举例三题一起来说说:
【例一】(如图)在△ABC中,取其内一点D,使得:DA=DB=DC,过D作线段MN,交AB于点M交BC于点N,若:∠CAB=45º,DM=√7,∠DAM=∠CDN,BN=3CN,求:线段DN的长
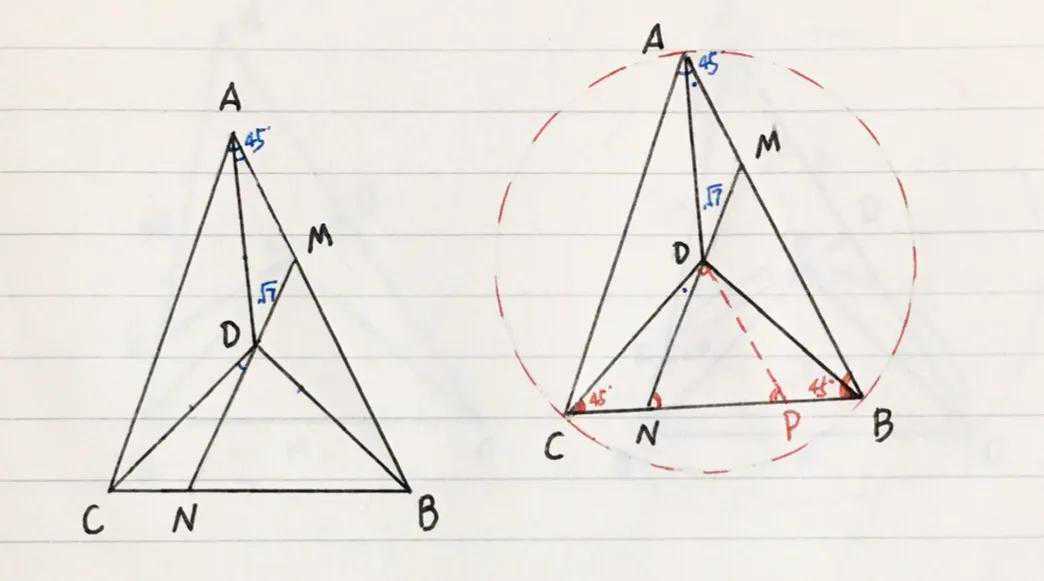
【分析】作辅圆(作△ABC的外接圆⊙D)
(1)由已知可得:点D为△ABC的外心,作其的外接圆⊙D,∴圆心角:∠BDC=2∠CAB=90º,∴∠BCD=∠CBD=45º,∠DBA=∠DAB=∠CDN
(2)∠MNB=45º+∠CDN,∠MBN=45º+∠DBA,∴∠MNB=∠MBN,∴MN=MB
(3)过点D作DP∥MB交CB于点P,则DN=DP,易证:△CDN≌△BDP,∴CN=PB,PB=BN/3,即:NP:PB=2:1
(4)由DP∥MB,∴ND/DM=NP/PB=2/1,∴DN=2DM=2√7,即:线段DN的长为2√7
【例二】(如图)在△ABC中,∠BAC=60º,BC=11,点D、E分别在边BC与AB上,且满足:AD=DB=BE=8,点F为BD间一点,连EF,且:∠EFC=∠C,求线段EF的长
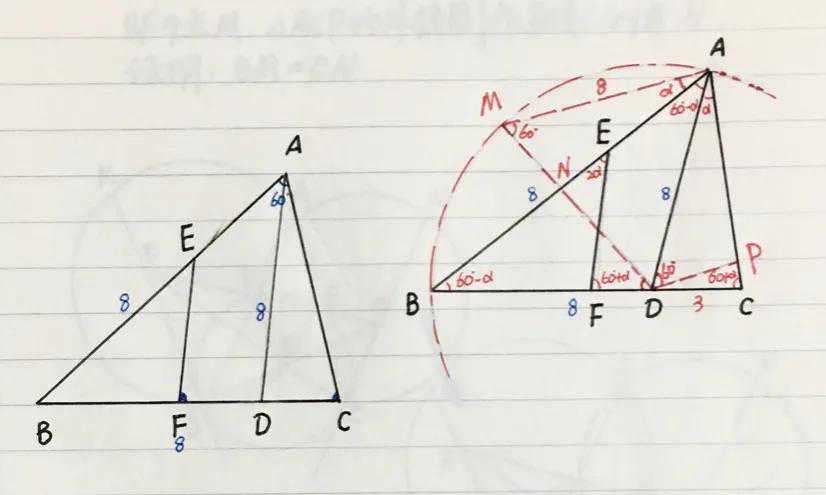
【分析】造隐圆(以D为圆心DA为半径作圆)
(1)由题意得:CD=11-8=3,设∠CAD=α,∴∠BAD=∠ABD=60º-α,∠C=60º+α=∠EFC,得:∠BEF=2α
(2)以点D为圆心,DA=DB=8的长为半径作圆⊙D,以DA为边如图作正△ADM,则点M在⊙D上,且∠BAM=α,∴∠BDM=2∠BAM=2α
(3)设MD交AB于点N,易证△DBN≌△EBF,∴EF=DN=DM-MN=8-MN
(4)如图作∠ADP=60º,边DP交AC于一点P,∴∠DPC=60º+α=∠C,∴PD=CD=3,易证:△ADP≌△AMN,∴MN=PD=3,EF=8-MN=5
(5)即:线段EF的长为5
【例三】(如图)正方形ABCD中,E点在CD上,连接BE,点F在BE上,使∠BAF=2∠CBE,且GF⊥BE交BC的延长线于点G,交CD于点H,若:EH=2,BC=7.5,求:线段CG的长
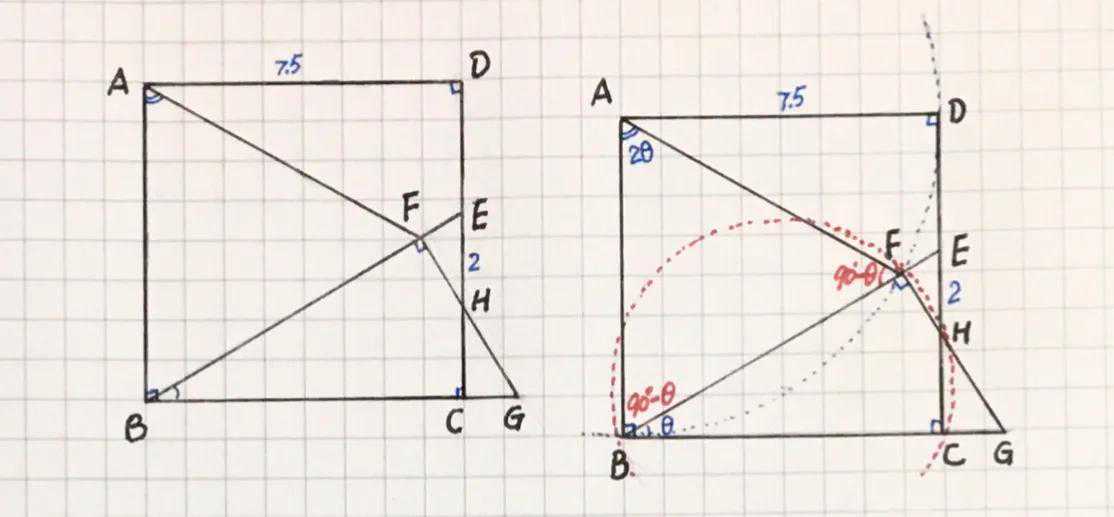
【分析】找隐圆(点在⊙A上半径为AB)
(1)设∠FBC=θ,则∠BAF=2θ,由已知导角得:∠ABF=90º-θ=∠AFB,∴AB=AF=AD
(2)以A为圆心,以AB的长为半径作⊙A,则点B、F、D匀在⊙A上,ED为圆的切线,由切割线定理得:DE²=EF×EB,易得:B、C、H、F四点共圆,由割线定理得:EF×EB=EH×EC,可得:DE²=EH×EC,整理:DE²+2DE-15=0,解得:DE=3,∴HC=2.5,CE=4.5
(3)由上易证得:Rt△CGH∽Rt△CEB,∴CG/CH=CE/CB,CG=4.5×2.5/7.5=1.5
(4)故:线段CG的长为:1.5
以上三例之分析,“道听度说”供参考。